Python SciPy Tutorial - Ein Leitfaden für Anfänger

Einführung

Computing ist ein wesentlicher Bestandteil der wissenschaftlichen Forschung. Mathematische, ingenieurwissenschaftliche, naturwissenschaftliche und andere technische Probleme sind komplex und erfordern Rechenleistung und -geschwindigkeit. Python bietet die SciPy-Bibliothek zum rechnerischen Lösen technischer Probleme.

Dieser Artikel stellt ein SciPy-Tutorial und die Implementierung des Codes in Python mit Beispielen vor.

Voraussetzungen

• Python 2.7 oder Python 3 installiert
• Eine Python-Umgebung zum Ausführen des Codes.
• SciPy-Bibliothek installiert.
• NumPy-Bibliothek installiert (Folgen Sie unserer Anleitung:So installieren Sie NumPy).
• Matplotlib-Bibliothek zum Plotten installiert (optional).

Was ist SciPy?

SciPy (Sci entific Py thon) ist ein wissenschaftliches Open-Source-Computing-Modul für Python. Basierend auf NumPy enthält SciPy Tools zur Lösung wissenschaftlicher Probleme. Wissenschaftler haben diese Bibliothek erstellt, um ihren wachsenden Bedarf an der Lösung komplexer Probleme zu decken.

SciPy vs. NumPy

Die NumPy-Bibliothek (Num Eric Py thon) führt numerische Berechnungen durch. Wissenschaftler verwenden diese Bibliothek für die Arbeit mit Arrays, da NumPy elementare Anwendungen in Datenwissenschaft, Statistik und Mathematik abdeckt.

SciPy deckt fortgeschrittene Berechnungen und Funktionen ab. Diese Bibliothek fügt weitere datenwissenschaftliche Funktionen, alle Funktionen der linearen Algebra und wissenschaftliche Standardalgorithmen hinzu.

Warum SciPy verwenden?

Die SciPy-Bibliothek baut auf NumPy auf und arbeitet mit Arrays. Die Rechenleistung ist schnell, da NumPy C zur Auswertung verwendet.

Der wissenschaftliche Python-Stack ähnelt MATLAB, Octave, Scilab und Fortran. Der Hauptunterschied besteht darin, dass Python einfach zu lernen und zu schreiben ist.

SciPy-Unterpakete

Die SciPy-Bibliothek hat verschiedene Gruppen von Unterpaketen. Es gibt zwei Möglichkeiten, Unterpakete aus dem SciPy-Modul zu importieren:

import scipy.<sub package name> as <alias>

Oder alternativ:

from scipy import <sub package name> as <alias>

Bei beiden Importmethoden ist der Alias ​​optional.

SciPy-Funktionen

SciPy enthält viele der primären Array-Funktionen, die in NumPy verfügbar sind, und einige der häufig verwendeten Module aus den SciPy-Unterpaketen.

Um eine Funktion aus einem Unterpaket zu importieren, verwenden Sie:

from scipy.<subpackage> import <function>

Grundfunktionen

Um Hilfe und Informationen zu jeder SciPy-Funktion zu erhalten, verwenden Sie help() Befehl:

help(<name of function>)

Die help() Der Befehl benötigt keine Parameter. Nach der Ausführung ohne Parameter erscheint eine Eingabeaufforderung, wo Sie den Funktionsnamen eingeben.

Eine weitere schnelle Möglichkeit, Hilfe zu einem beliebigen Befehl in Python zu erhalten, besteht darin, den Befehlsnamen zu schreiben, ein Fragezeichen an das Ende zu setzen und den Code auszuführen.

Sonderfunktionen

Spezielle Funktionen im SciPy-Modul umfassen häufig verwendete Berechnungen und Algorithmen. Alle Sonderfunktionen akzeptieren NumPy-Arrays als Eingabe. Die Berechnungen erfolgen elementweise.

Zum Importieren des special Unterpaket, verwenden Sie:

import scipy.special as special

Oder alternativ:

from scipy import special

Um eine bestimmte Funktion aus dem special zu importieren Unterpaket, verwenden Sie:

from scipy.special import <function name>

Fakultät

Bewerten Sie die Fakultät einer beliebigen Zahl, indem Sie Folgendes ausführen:

special.factorial(<integer or array>)

Um beispielsweise die Fakultät von zehn zu finden, verwenden Sie:

special.factorial(10)

Permutationen und Kombinationen

Um die Anzahl der Permutationen zu finden, verwenden Sie:

special.perm(<number of elements>, <number of elements taken>)

Zum Beispiel, um die Anzahl der Permutationen von drei Elementen zu sehen, die jeweils zu zweit genommen werden:

special.perm(6,2)

Finden Sie auf ähnliche Weise die Anzahl der Kombinationen mit:

special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)

Geben Sie Folgendes ein, um die Anzahl der Kombinationen von drei Elementen zu ermitteln, die jeweils zu zweit mit Wiederholung aufgenommen wurden:

special.comb(6,2, repetition=True)

Permutationen und Kombinationen werden in Sortieralgorithmen der Informatik verwendet.

Exponentialfunktionen

Exponentialfunktionen werten die Exponenten für verschiedene Basen aus.

Berechnen Sie die Exponenten der Basis zehn mit:

special.exp10(<integer or array>)

Zum Beispiel:

special.exp10([0,1,2])

Die Informatik verwendet häufig Exponentialfunktionen zur Basis zwei:

special.exp2(<integer or array>)

Berechnen Sie die Zehnerpotenz der Basis zwei mit:

special.exp2(10)

Logarithmische Summe von Exponentialen

Die logarithmische Summe der Exponentiale (LSE oder LogSumExp) ist eine Annäherung, die von maschinellen Lernalgorithmen verwendet wird. Berechnen Sie die LSE mit:

special.logsumexp(<integer or array>)

Bessel-Funktion

Bessel-Funktionen treten bei der Wellenausbreitung, Signalverarbeitung und statischen potenziellen Problemen auf. Finden Sie die Bessel-Funktion erster Art mit:

special.jn(<integer order>, <integer or array>)

Nutzen Sie den vollen Stack, um die Bessel-Funktion zu visualisieren. Um die Bessel-Funktion zweiter Ordnung erster Art zu finden, verwenden Sie:

#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)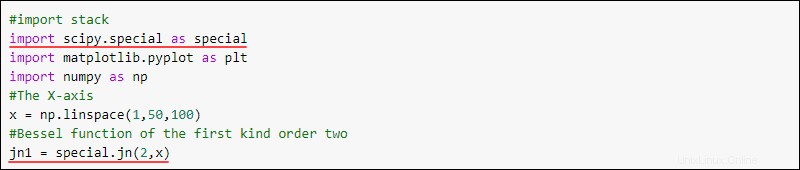

Zeichnen Sie die Ergebnisse auf:

#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)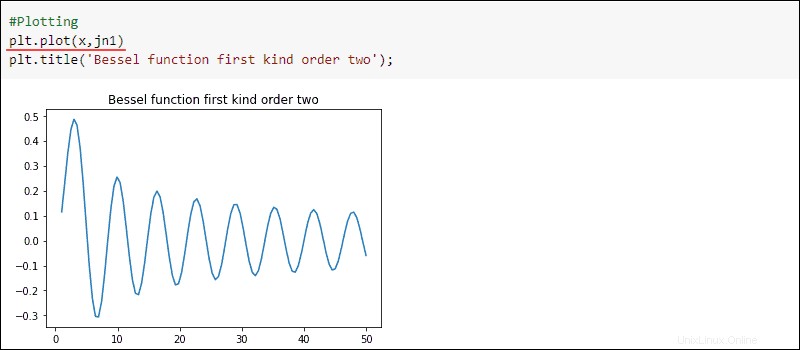

Integration und ODE-Funktionen

SciPy stellt ein Unterpaket für Berechnungen mit bestimmten Integralen zur Verfügung. Zum Importieren der integrate Unterpaket, verwenden Sie:

import scipy.integrate as integrate

Oder alternativ:

from scipy import integrate

Importieren Sie eine bestimmte Funktion aus dem Unterpaket integrate mit:

from scipy.integrate import <function name>

Allgemeine Integration

Berechnen Sie ein einzelnes Variablenintegral mit dem quad Funktion aus integrate Unterpaket:

integrate.quad(<function>, <lower limit>, <upper limit>)

Die function Die Eingabe wird mit einer Lambda-Funktion definiert.

Zum Beispiel, um das bestimmte Integral der Funktion x+1 zwischen Null und Eins zu berechnen:

from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)

Die Ausgabe zeigt zwei Werte. Der erste Wert ist das berechnete Integral, der zweite der Schätzfehler.

Optimierungsfunktionen

SciPy hat ein Optimierungs-Unterpaket zum Finden des Minimums oder Maximums einer Funktion. Die optimize Unterpaket enthält Löser und Algorithmen zum Finden lokaler und globaler Optimalwerte.

So importieren Sie das Optimierungs-Unterpaket:

from scipy import optimize

Oder verwenden Sie:

import scipy.optimize as optimize

Um eine bestimmte Funktion aus dem Unterpaket optimize zu importieren , ausführen:

from scipy.optimize import <function name>

Funktion minimieren

Das Finden eines Minimums einer Funktion wird beim maschinellen Lernen verwendet, um den Verlust (oder Fehler) eines Algorithmus zu verringern.

Sie können beispielsweise eine Funktion erstellen und das Minimum finden. Verwenden Sie dazu den fmin Funktion aus optimize Unterpaket in SciPy:

#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
    return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)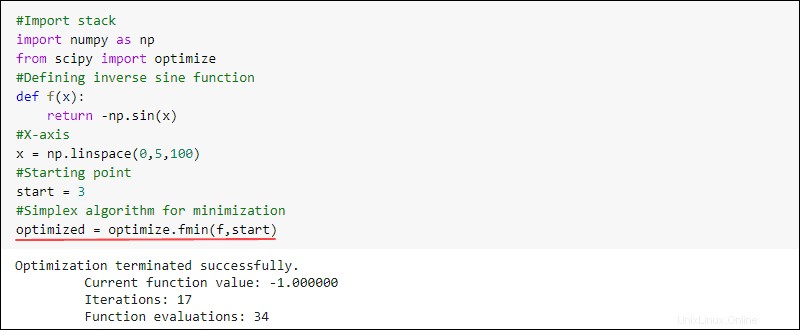

Um das Ergebnis zu plotten, führen Sie Folgendes aus:

import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])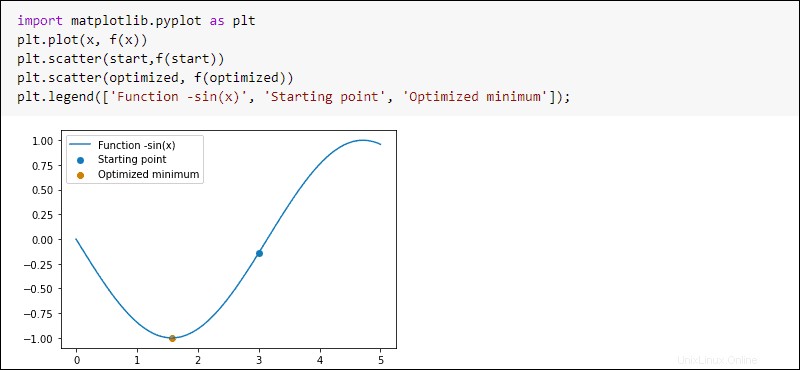

Fourier-Transformationsfunktionen

SciPy enthält ein Unterpaket für Fourier-Transformationsfunktionen namens fftpack . Die Transformationen sind diskrete Fourier-Transformationen (DFT). Alle Transformationen werden mit dem Algorithmus Fast Fourier Transformation (FFT) angewendet.

Um das fftpack zu importieren Unterpaket, verwenden Sie:

import scipy.fftpack as fftpack

Oder:

from scipy import fftpack

Schnelle Fourier-Transformation

Erstellen Sie als Beispiel eine periodische Funktion als Summe von drei Sinuswellen:

import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3

Zeichnen Sie die Wellen mit matplotlib :

import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');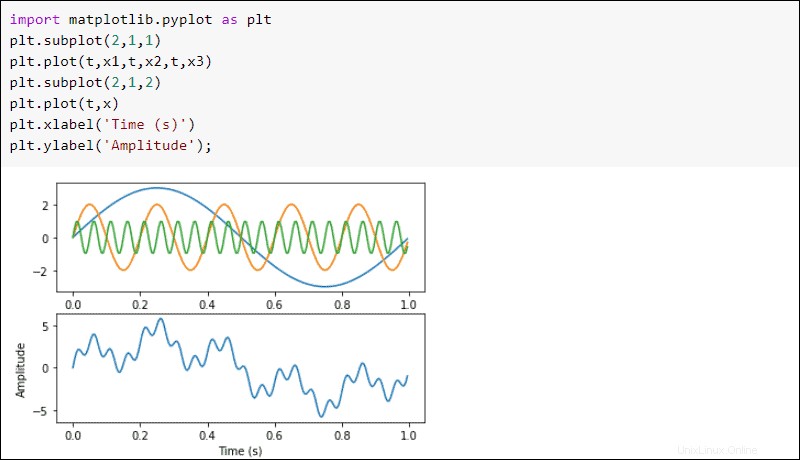

Als nächstes wenden Sie fft an und fftfreq Funktionen aus dem fftpack um eine Fourier-Transformation des Signals durchzuführen.

from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2

Zeichnen Sie die Ergebnisse, um den Frequenzbereich anzuzeigen:

plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()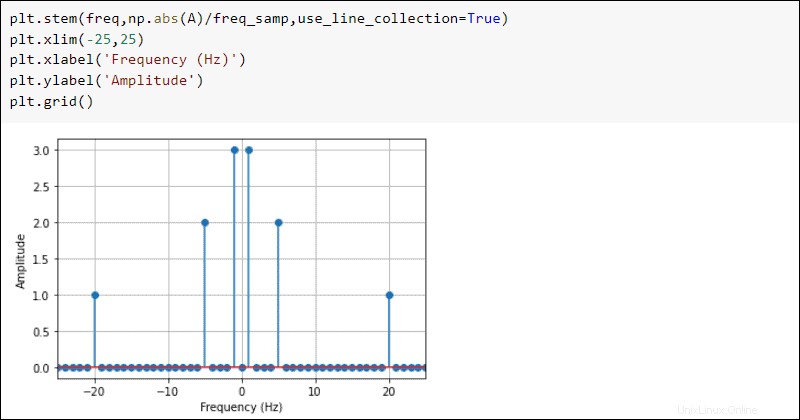

Signalverarbeitungsfunktionen

Das Unterpaket signal enthält Funktionen, die in der Signalverarbeitung verwendet werden. Zum Importieren von signal , ausführen:

import scipy.signal as signal

Oder alternativ:

from scipy import signal

Faltung

Eine häufige Aufgabe in der Signalverarbeitung ist die Faltung. Das SciPy-Unterpaket signal hat die Funktion convolve um diese Aufgabe zu erfüllen. Erstellen Sie beispielsweise zwei Signale mit unterschiedlichen Frequenzen:

import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)

Plotten Sie die Signale:

import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')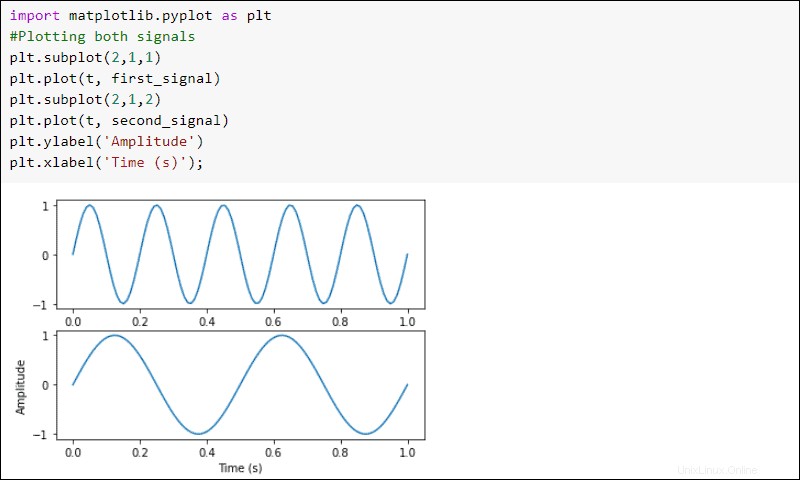

Importieren Sie das signal Unterpaket von scipy . Verwenden Sie convolve Funktion aus dem signal Unterpaket, um die beiden Signale zu falten:

#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')

Zeichnen Sie die Ergebnisse auf:

#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')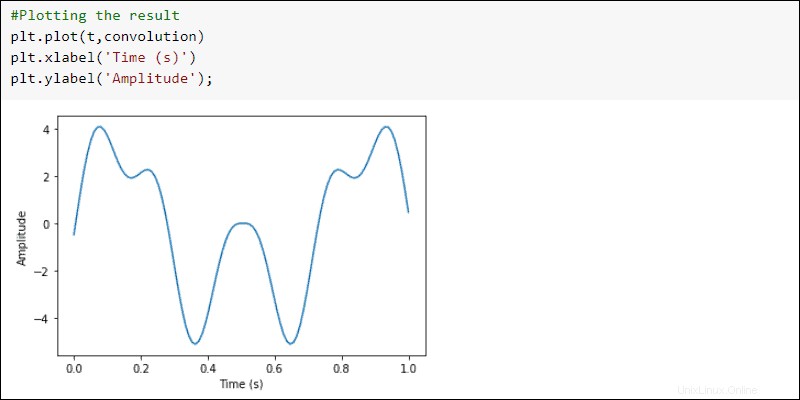

Interpolationsfunktionen

Interpolation wird im Bereich der numerischen Analyse verwendet, um Werte zwischen zwei Punkten zu verallgemeinern. SciPy hat die interpolate Unterpaket mit Interpolationsfunktionen und Algorithmen.

Importieren Sie die interpolate Unterpaket mit:

import scipy.interpolate as interpolate

Oder:

from scipy import interpolate

Eindimensionale Interpolation

Die SciPy interpolate Unterpaket hat den interp1d Funktion zur eindimensionalen Interpolation von Daten. Erstellen Sie beispielsweise Spielzeug Daten mit numpy :

import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)

Interpolieren Sie die Daten mit interp1d aus der interpolate Unterpaket:

from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)

Zeichnen Sie die Ergebnisse auf:

#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])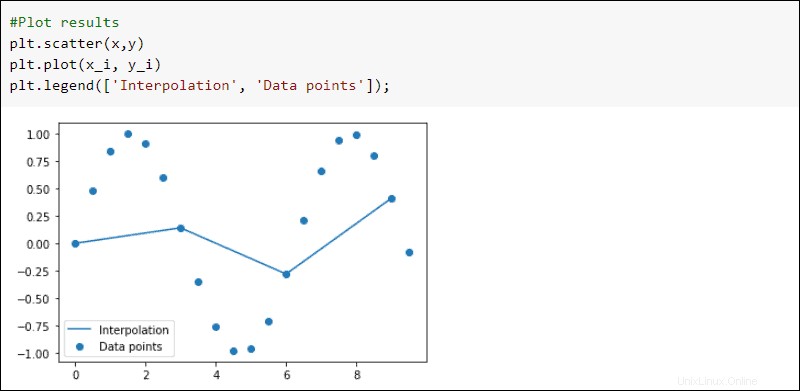

Lineare Algebra

SciPy verfügt über ein voll funktionsfähiges Unterpaket für lineare Algebra. Das SciPy-Unterpaket für lineare Algebra ist mit den ATLAS LAPACK- und BLAS-Bibliotheken für schnellere Berechnungen optimiert.

Um das Paket für lineare Algebra aus SciPy zu importieren, führen Sie Folgendes aus:

import scipy.linalg as linalg

Oder verwenden Sie:

from scipy import linalg

Alle Funktionen der linearen Algebra erwarten ein NumPy-Array als Eingabe.

Determinante

Berechnen Sie die Determinante einer Matrix mit det aus dem linalg Unterpaket:

linalg.det(<numpy array>)

Zum Beispiel:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)

Inverse Matrix

Bestimmen Sie die inverse Matrix mit inv :

linalg.inv(<numpy array>)

Zum Beispiel:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)

Eigenvektoren und Eigenwerte

Eigenvektoren und Eigenwerte sind eine Matrixzerlegungsmethode. Das Eigenwert-Eigenvektor-Problem ist ein häufig implementiertes Problem der linearen Algebra.

Das eig Funktion findet die Eigenwerte und Eigenvektoren einer Matrix:

linalg.eig(<numpy array>)

Die Ausgabe gibt zwei Arrays zurück. Der erste enthält Eigenwerte und der zweite Eigenvektoren für die gegebene Matrix. Zum Beispiel:

import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)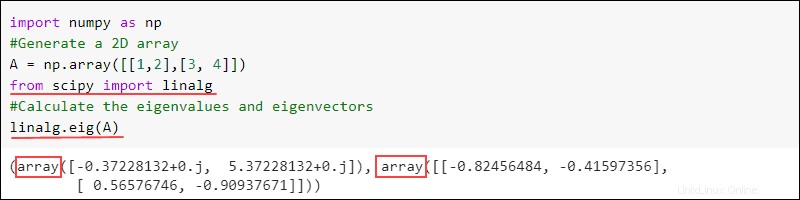

Räumliche Datenstrukturen und Algorithmen

Räumliche Datenstrukturen sind Objekte aus Punkten, Linien und Flächen. SciPy verfügt über Algorithmen für räumliche Datenstrukturen, da sie für viele wissenschaftliche Disziplinen gelten.

Importieren Sie spatial Unterpaket von SciPy mit:

import scipy.spatial as spatial

Oder:

from scipy import spatial

Ein bemerkenswertes Beispiel für einen räumlichen Algorithmus ist das Voronoi-Diagramm. Für einen gegebenen Satz von Punkten unterteilen Voronoi-Karten eine Ebene in Regionen. Wenn ein neuer Punkt in eine Region fällt, ist der Punkt in der Region der nächste Nachbar.

Erstellen Sie als Beispiel ein Voronoi-Diagramm aus zwanzig zufälligen Punkten:

from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)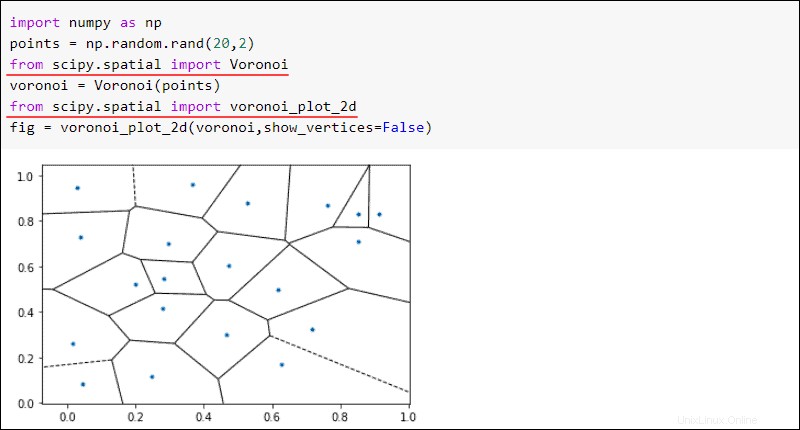

Bildverarbeitung

SciPy hat ein Unterpaket für verschiedene n-dimensionale Bildverarbeitung. So importieren Sie das ndimage Unterpaket, führe aus:

import scipy.ndimage as ndimage

Oder verwenden Sie:

from scipy import ndimage

Das SciPy misc Unterpaket enthält ein Beispielbild zu Demonstrationszwecken. Um die Datei misc zu importieren Unterpaket und zeige das Bild:

from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()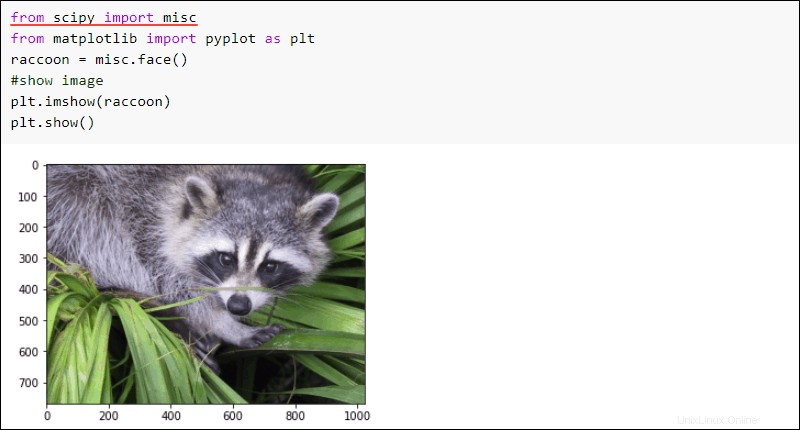

Importieren Sie das ndimage Unterpaket und wenden Sie einen uniform_filter an zum Bild. Zeigen Sie das Bild, um die Ergebnisse zu sehen:

from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)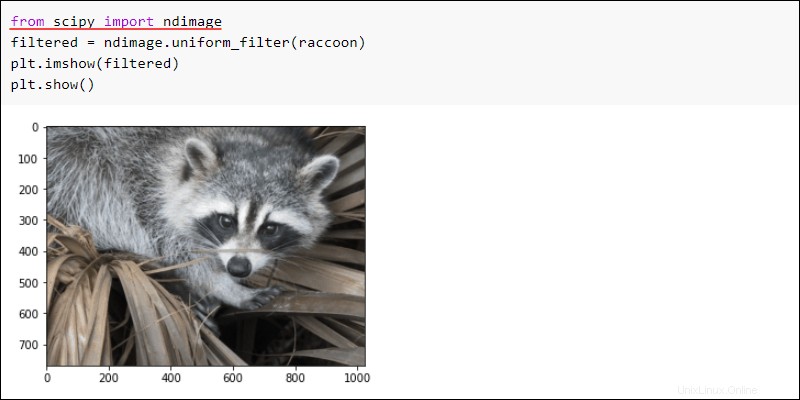

File IO (File Input / Output Package)

SciPy hat ein Unterpaket für die Dateieingabe und -ausgabe namens io . Das io Unterpaket wird zum Lesen und Schreiben von Datenformaten aus verschiedenen wissenschaftlichen Rechenprogrammen und Sprachen wie Fortran, MATLAB, IDL usw. verwendet.

Importieren Sie io Unterpaket von SciPy mit:

import scipy.io as sio

Oder verwenden Sie:

from scipy import io as sio