In diesem Tutorial besprechen wir die Vektoralgebra und entsprechende Berechnungen unter Scientific Linux. Für unseren Zweck habe ich Python als Programmiersprache wegen seiner Einfachheit und Rechenleistung gewählt. Jede Linux-Distribution hat standardmäßig einen Python-Editor/Compiler, der über ein Terminalfenster aufgerufen wird. Gehen wir einige Konzepte der Vektoralgebra durch.
Hinweis:Wir werden nur im realen Raum von zwei oder drei Dimensionen arbeiten.
Vektoralgebra
Das Element eines Vektorraums kann aus mathematischer Sicht als die Anordnung einer Anzahl von Elementen dargestellt werden, die zu diesem Vektorraum gehören. Genauer gesagt, und im numerischen Rechenansatz, kann es als eine Liste reeller Zahlen dargestellt werden, die drei grundlegende Eigenschaften hat:
Größe
Die Größe des Vektors und wird mit dargestellt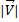 
; dies ist der skalare Teil eines Vektors. Um den Betrag eines Vektors zu berechnen, müssen wir die folgende Formel ausführen:
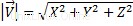
X, Y und Z sind die Vektorkoordinaten.
Richtung
Die Richtung eines Vektors wird durch eine Leitlinie angegeben, die für jede Achse des Koordinatensystems einen bestimmten Winkel hat, der als Richtungswinkel bezeichnet wird.
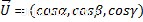
Wo Alpha, Beta und Gamma die Vektorrichtungswinkel und ihre Kosinusse die Richtungskosinusse sind, können sie auch berechnet werden, indem jede Vektorkoordinate durch ihre Größe geteilt wird.
Orientierung
Eine der beiden möglichen Ausrichtungen zwischen derselben Richtung.
Vektoralgebraische Summe
Um eine algebraische Summe von Vektoren zu bilden, müssen wir die homologen Koordinaten zweier Vektoren addieren, wobei die gleichen Eigenschaften der algebraischen Summe reeller Zahlen beachtet werden. Einfach so:
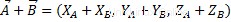Wie wir sehen können, ist das Ergebnis ein weiterer Vektor, der zum selben Vektorraum gehört.
Produkt eines Vektors durch einen Skalar
Bei einem Vektor und einem Skalar ist das Produkt Vektor durch Skalar als Skalarprodukt jeder Koordinate des Vektors definiert:
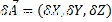
Wo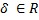 
Einheitenvektor
Eine direkte Anwendung für den Produktvektor durch einen Skalar ist der Einheitsvektor a Einheitsvektor ist ein normierter Vektor der Länge 1.
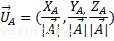
Lineare Kombination
Wenn wir die vergangenen Operationen, algebraische Summe und Produktvektor-Skalar mischen, erhalten wir eine Linearkombination, bei der das Ergebnis auch ein Vektor ist, der zum selben Vektorraum gehört, wie ist:
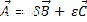
Wobei Vektor A eine Linearkombination von Vektoren B ist und C.
Python auf Scientific Linux 7.1
Um die Vektoralgebra zu implementieren, haben wir Python als Berechnungssprache gewählt. Der von uns gewählte Texteditor ist gedit und wird standardmäßig mit der Distribution Scientific Linux 7.1 geliefert.
Größe eines Vektors
Rufen wir gedit über ein Terminal auf oder klicken Sie einfach auf das Symbol auf der Registerkarte Anwendungen:
Zunächst müssen wir mit Listen arbeiten, die Vektoren darstellen und als deklariert werden sollten ist:
V=[2, 2, 1]
Lassen Sie uns eine Variable deklarieren, um die Größe zu speichern und einen Wert zu geben, wir verwenden 0.
modV=0
Jetzt verwenden wir die Klasse math, um die Quadratwurzel zu berechnen:
import math
Die Berechnung der Magnitude:
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
Wie wir sehen können, müssen wir den Unterindex verwenden, um das Element aus der Liste anzugeben, das wir bearbeiten werden, beginnend bei 0.
Das vollständige Skript lautet wie folgt:
V=[2, 2, 1]
modV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
print (modV)
Sobald wir fertig sind, müssen wir die Datei mit der Erweiterung .py speichern und den Dateipfad suchen und dort mit der rechten Maustaste ein Terminalfenster öffnen und dann "Im Terminalfenster öffnen". Nachdem wir den Python-Interpreter aufgerufen haben, geben Sie Folgendes ein:
$ python [path]/yourfilename.py
Dies öffnet ein Fenster wie dieses und gibt das Ergebnis aus:
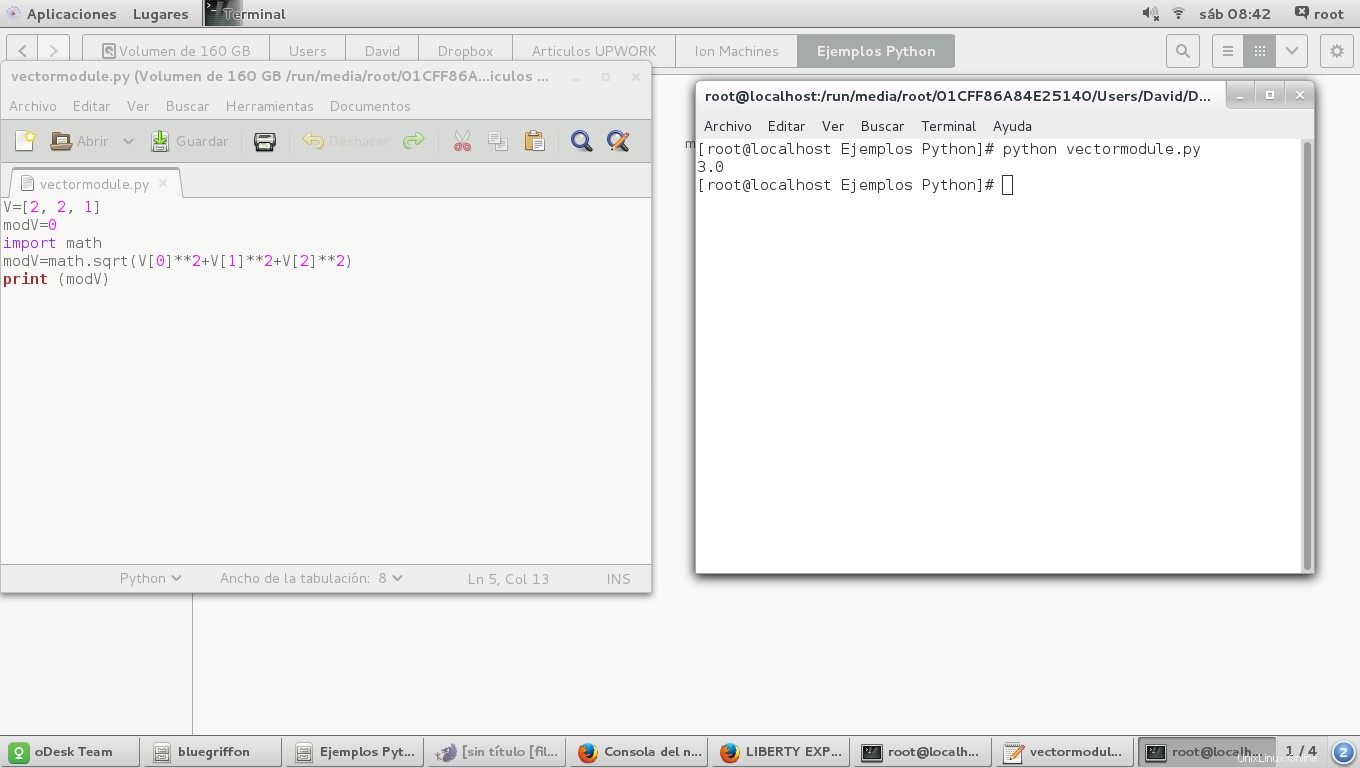
Eine andere Möglichkeit ist die Verwendung einer for-Schleife wie dieser:
for x in range (0,3):
modV+=V[x]**2
modV=math.sqrt(modV)
Hier müssen wir Einrückungstechniken verwenden, da der Python-Interpreter auf diese Weise arbeitet.
Richtung eines Vektors
Verwenden Sie die Klasse math
V=[2, 1, 2]
modV=0
import math
for x in range (0,3): #loop for calculating the magnitude
modV+=V[x]**2
modV=math.sqrt(modV)
for y in range (0,3): #loop for calculating the director cosines
V[y]=V[y]/modV
print (V)
Das Ergebnis ist das nächste:
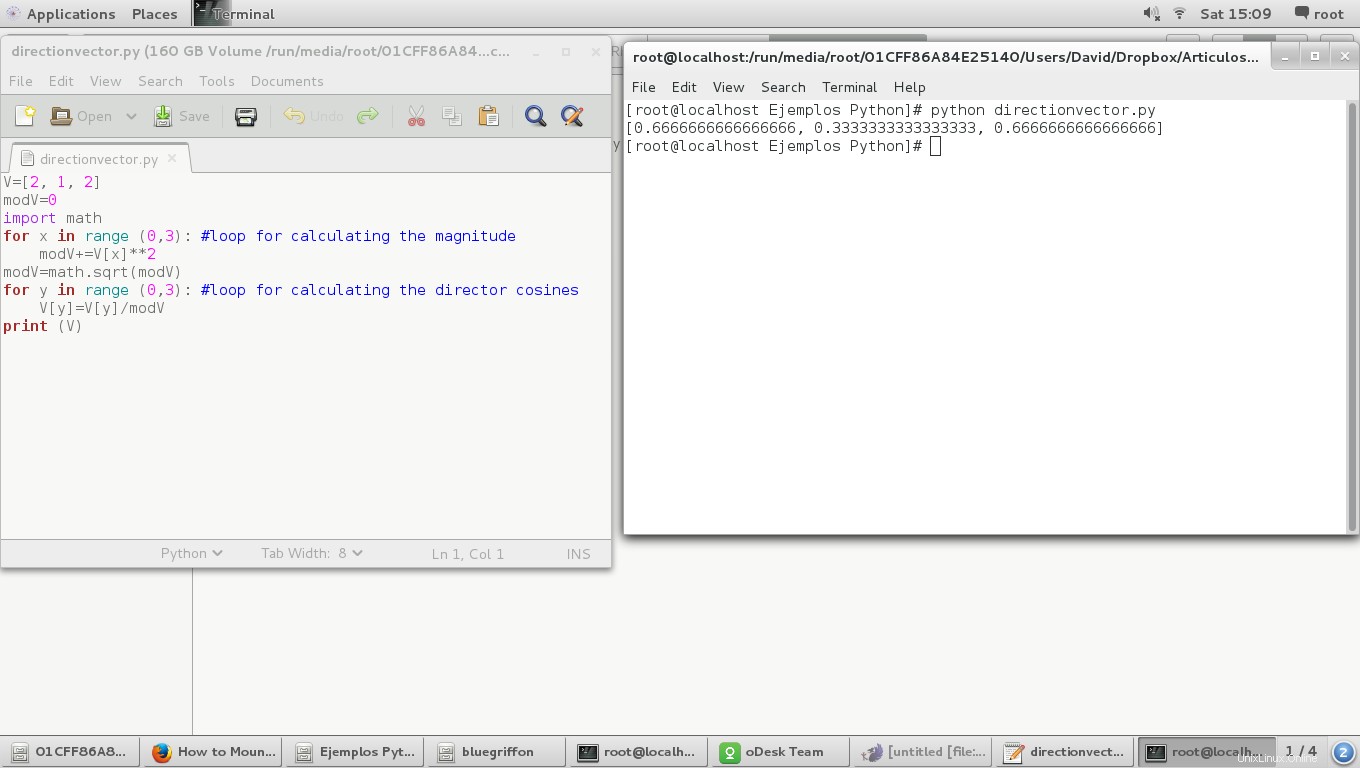
Eine andere Möglichkeit ist die Verwendung der trigonometrischen Funktionen des Mathematikunterrichts etwa so:
Berechnen wir zuerst die Richtungswinkel:
V=[2, 1, 2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))
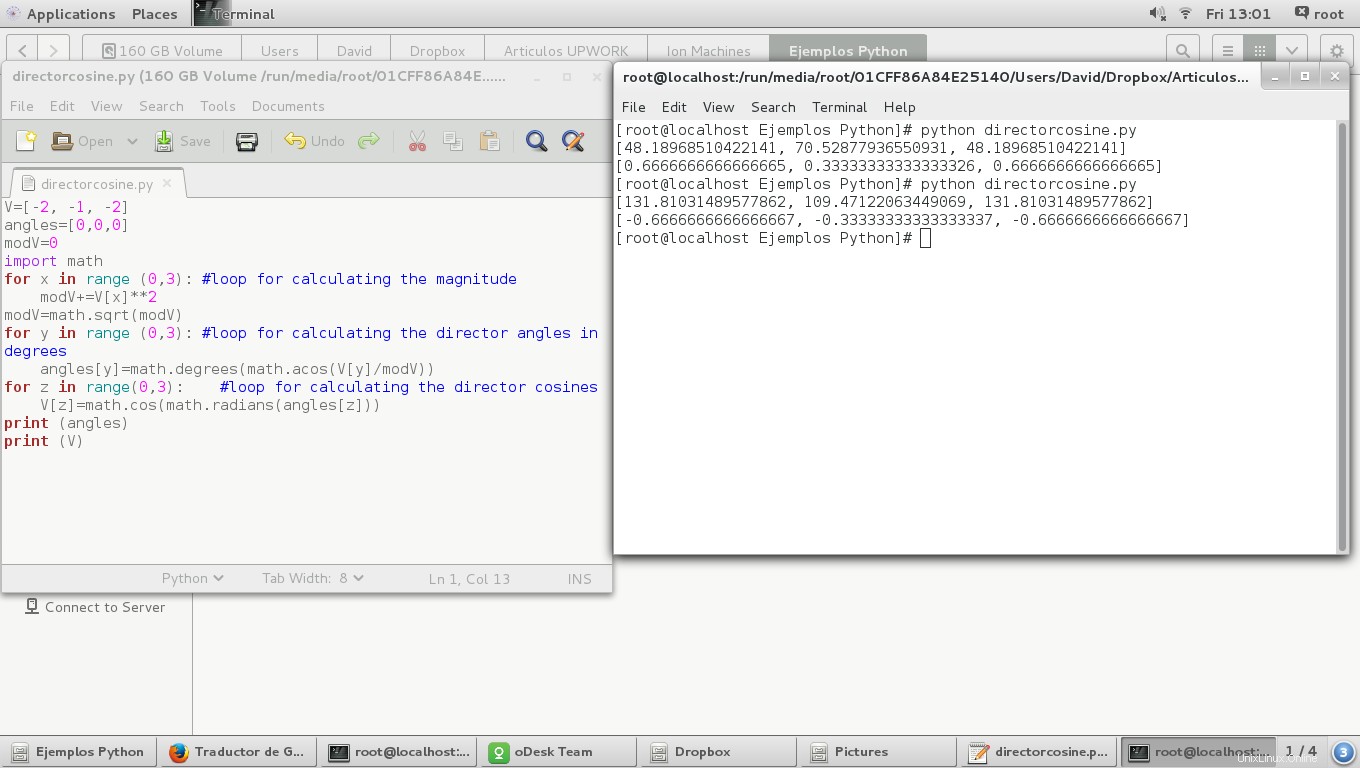
Und dann berechnen wir die Direktorkosinusse und drucken sie aus
for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
Und das Ergebnis:
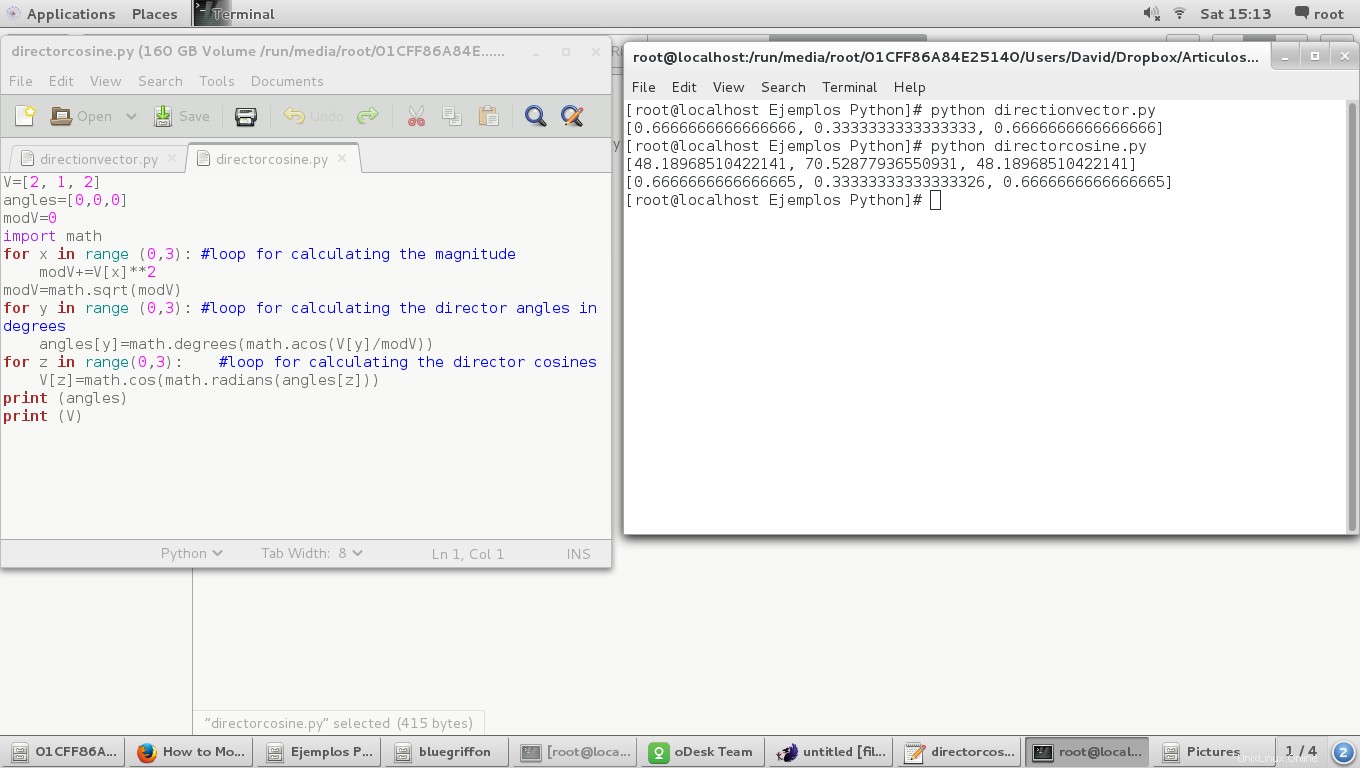
Wir können beobachten, dass die Direktorkosinusse denselben Wert haben
Orientierung eines Vektors
Wenn wir das Vorzeichen aller Koordinaten eines Vektors ändern, ändern wir von Natur aus die Ausrichtung des Vektors, wie folgt:
V=[-2, -1, -2]
angles=[0,0,0]
modV=0
import math
for y in range (0,3): #loop for calculating the director angles in degrees
angles[y]=math.degrees(math.acos(V[y]/modV))for z in range(0,3): #loop for calculating the director cosines
V[z]=math.cos(math.radians(angles[z]))
print (angles)
print (V)
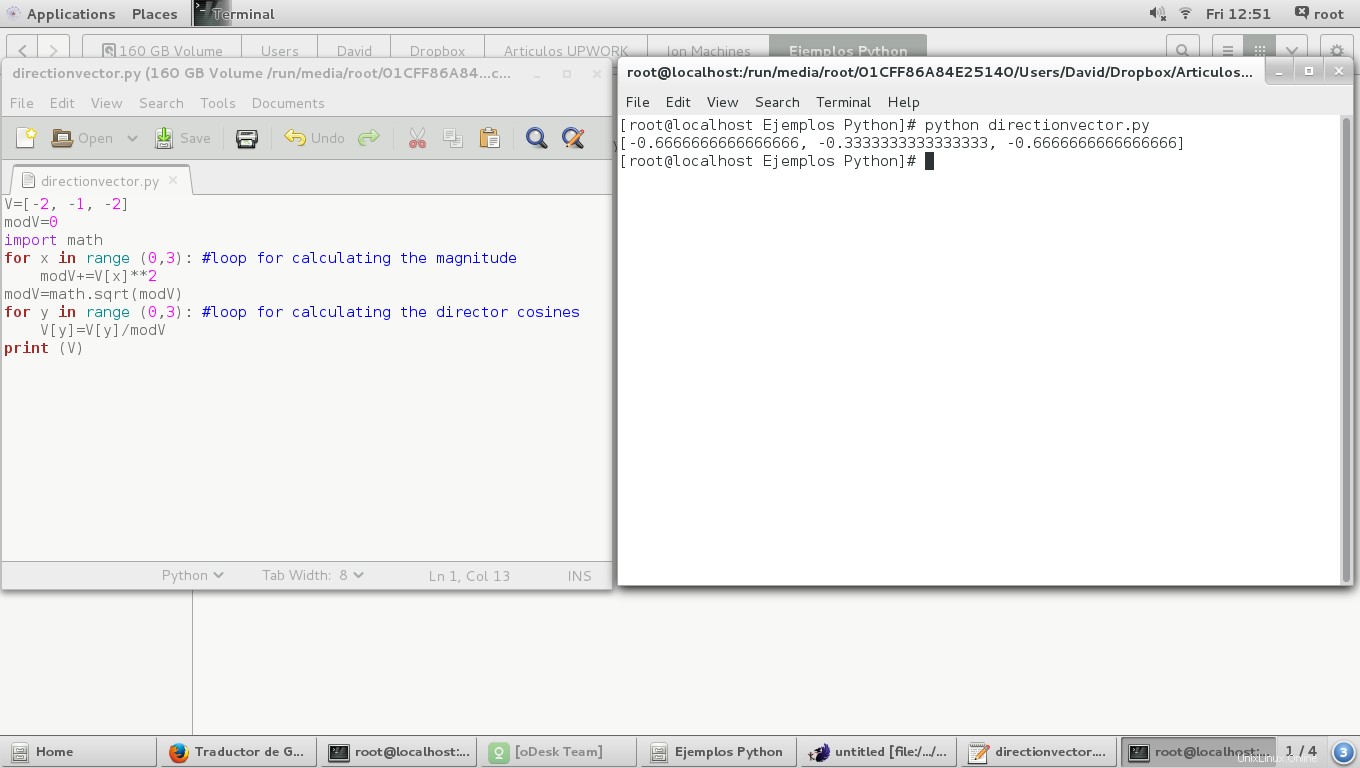
Im nächsten Bild können wir sehen, dass die Winkel des Direktors bei 180 Grad unterschiedlich sind von den Originalen
Vektoralgebraische Summe
Zuerst müssen wir alle an der algebraischen Summe beteiligten Vektoren wie folgt deklarieren:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
wo wir A plus B summieren und das Ergebnis in S speichern
Das Hinzufügen von zwei Vektoren (Listen) in Python entspricht dem Ausführen einer 'for'-Schleife für jede Koordinate des resultierenden Vektors, also müssen wir das nächste tun:
for x in range(0,3):
S[x]=A[x]+B[x]
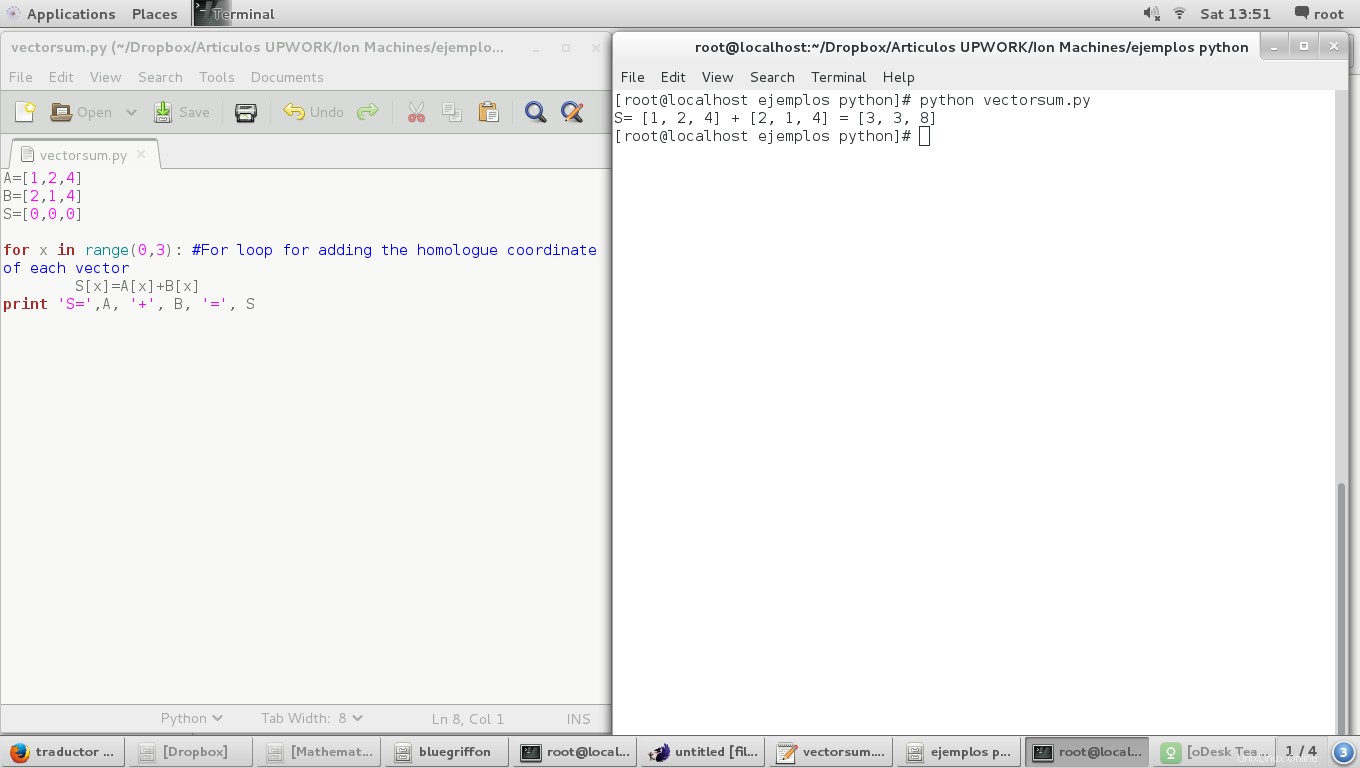
Hier haben wir das vollständige Skript für die algebraische Vektorsumme:
A=[1,2,4]
B=[2,1,4]
S=[0,0,0]
for x in range(0,3): #For loop for adding the homologue coordinate of each vector
S[x]=A[x]+B[x]
print 'S=',A, '+', B, '=', S
Und das Ergebnis ist:
Produkt eines Vektors durch einen Skalar
Gegebener Vektor:
A=[1,-2,3]
und ein Skalar:
scalar=-2
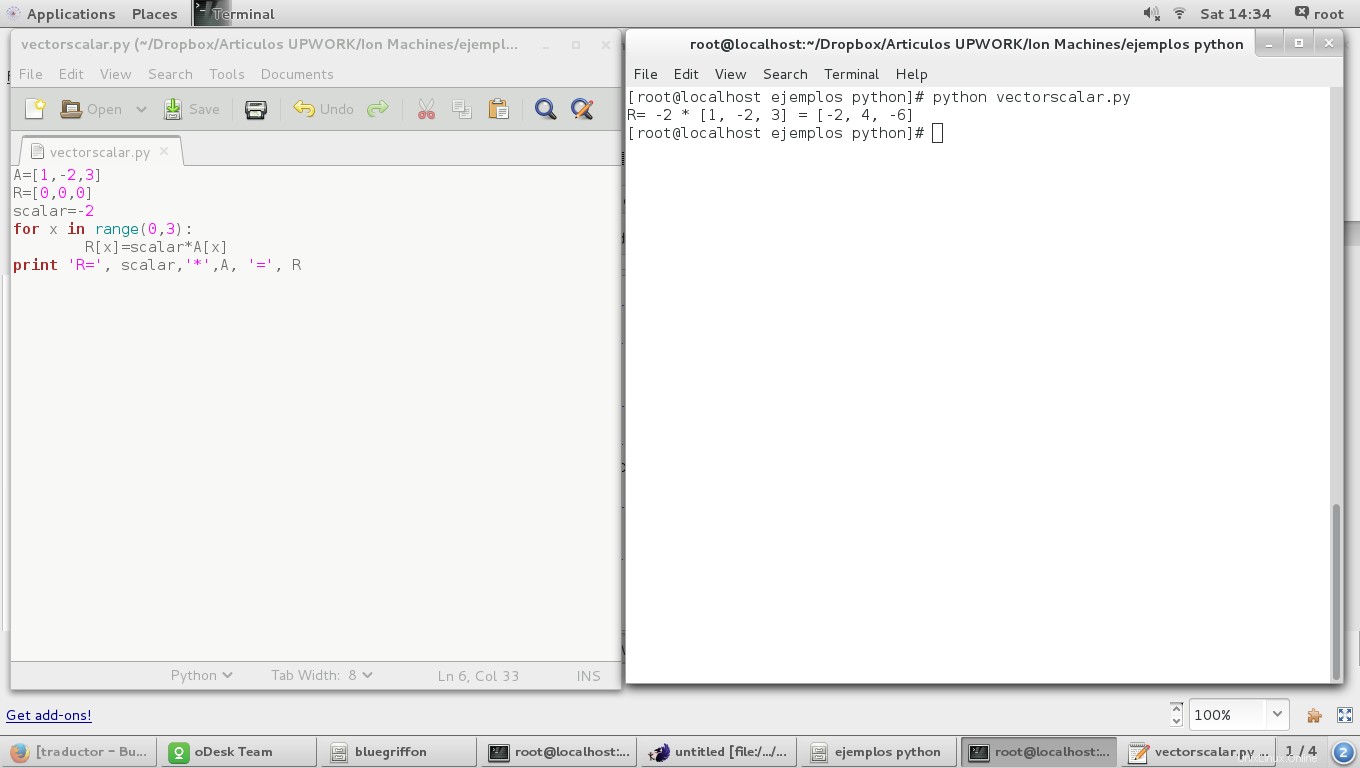
Produkt Vektor durch einen Skalar ist definiert als das Skalarprodukt jeder Koordinaten des Vektors:
for x in range(0,3):
R[x]=scalar*A[x]
und das Ergebnis ist:
Einheitenvektor
Mit dem Skript „Größe eines Vektors“ haben wir:
V=[2, 2, 1]
U=[0,0,0]
modV=0
invmodV=0
import math
modV=math.sqrt(V[0]**2+V[1]**2+V[2]**2)
invmodV=1/modV
for x in range(0,3):
U[x]=invmodV*V[x]
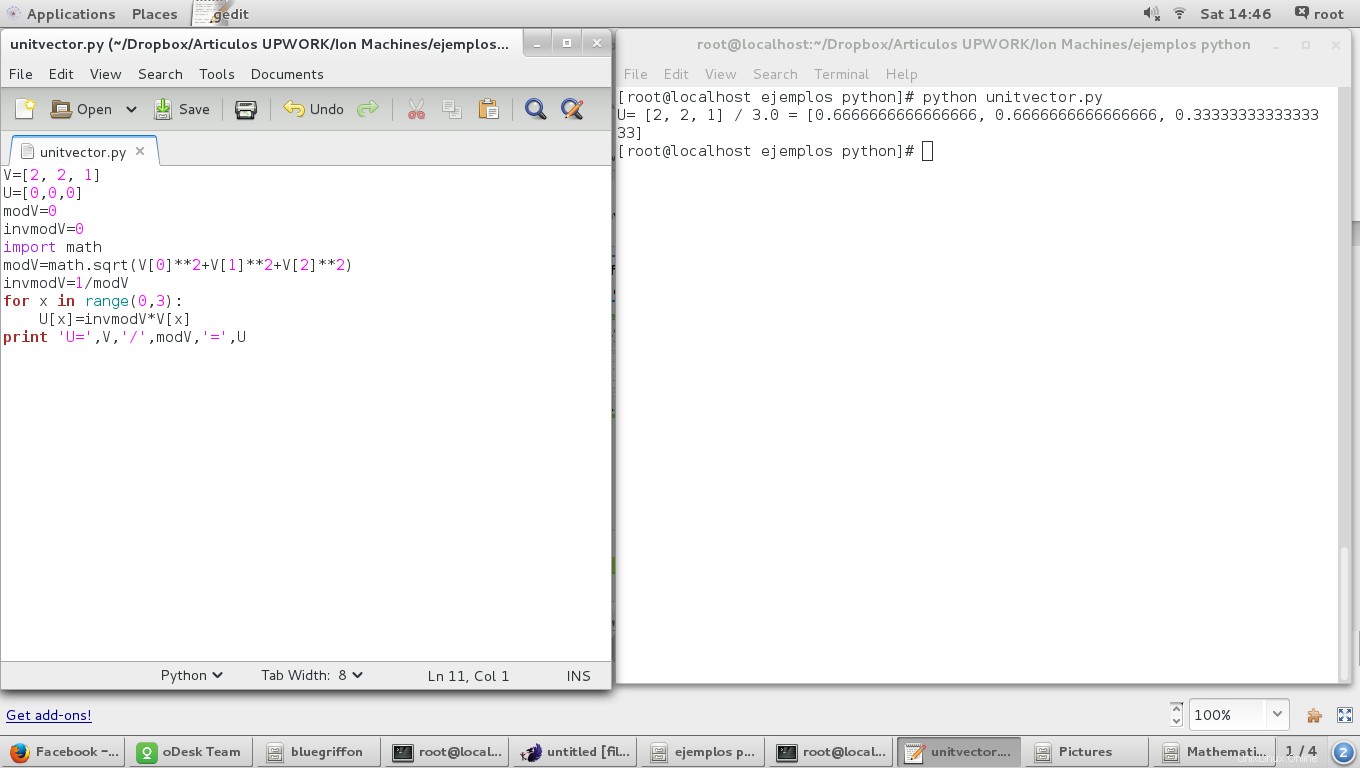
print 'U=',V,'/',modV,'=',U
und das Ergebnis ist:
Lineare Kombination
Ausgehend von drei Vektoren A, B und C können wir die Skalarwerte berechnen, die multipliziert mit B bzw. C den Vektor A ergeben. Mit anderen Worten, den Vektor A als lineare Kombination der Vektoren B und C platzieren :
A=[7, 9, -8]
B=[1, 3, -2]
C=[-2, 0, 1]
Eine Linearkombination führt zu einem Gleichungssystem, 3 Gleichungen mit 2 Variablen (Skalare) wenn drei Vektoren r3 oder 2 Gleichungen mit 2 Variablen wenn es zwei Vektoren in R3 sind, die sich durch Anwendung einer Determinante einer Matrix lösen lassen. Hier müssen wir wegen der von Python gehandhabten Datentypen einen Punkt machen. In vielen Fällen hat das Ergebnis bei der Berechnung der an einer Linearkombination beteiligten Skalare Nachkommastellen, was zu Gleitkommaoperationen führt. Die numerischen Datentypen, die von Python verarbeitet werden, sind:Integer, Real, Long. Wir müssen also die Koordinaten der Vektoren als Real-Datentyp einfügen, damit diese reelle Zahlen darstellen (Gleitkomma). Wir müssen einige Merkmale des Datentyps in Python kennen und verstehen:
- Integer benötigen weniger Speicherplatz als der Real-Typ.
- Operationen mit Real sind langsamer als Integer.
Hier haben wir die gleichen Vektoren, aber als Real-Typ deklariert:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
Damit können wir also die Vektoren vertauschen und haben somit immer die Systemlösung.
Als erstes müssen wir prüfen, ob es Koplanarität zwischen den Vektoren gibt oder nicht, also wissen, ob es da ist oder nicht ist eine Linearkombination. Dafür implementieren wir eine Determinantenmatrix:
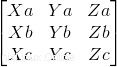
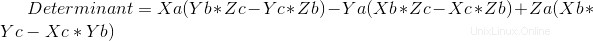
Code:
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
Ist diese Determinante gleich Null (0), so besteht eine lineare Abhängigkeit zwischen den Vektoren und wir können mit der Berechnung der Skalare fortfahren. Wie oben erwähnt, hat das Gleichungssystem drei Gleichungen mit zwei Variablen, was ein bestimmtes kompatibles System ergibt, für das wir zwei der drei Gleichungen nehmen und skalare Werte lösen müssen, dann mit der dritten Gleichung, die vorher nicht genommen wurde, überprüfen, ob die vorherige Skalarwerte lösen es. Wenn sie dies nicht lösen, gibt es keine Linearkombination.
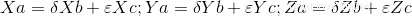
Hier haben wir den vollständigen Code:
A=[7.0,9.0,-8.0]
B=[1.0,3.0,-2.0]
C=[-2.0,0.0,1.0]
det0=A[0]*(B[1]*C[2]-B[2]*C[1])-A[1]*(B[0]*C[2]-B[2]*C[0])+A[2]*(B[0]*C[1]-B[1]*C[0]) #Main Determinant involving all vectors
if det0==0:
det1=B[0]*C[1]-B[1]*C[0] #First Determinant involving the first and second lines of the equations system
if det1==0:
det2=B[1]*C[2]-B[2]*C[1] #Second Determinant involving the second and third lines of the equations system
if det2==0:
print 'Linear Combination Unexistent'
else:
det3=A[1]*C[2]-A[2]*C[1]
det4=B[1]*A[2]-B[2]*A[1]
sc1=det3/det2
sc2=det4/det2
if sc1*B[0]+sc2*C[0]==A[0]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
det3=A[0]*C[1]-A[1]*C[0]
det4=B[0]*A[1]-B[1]*A[0]
sc1=det3/det1
sc2=det4/det1
if sc1*B[2]+sc2*C[2]==A[2]:
print 'Scalar 1 =', sc1, 'Scalar 2 =', sc2
print A,'=',sc1,'*',B,'+',sc2,'*',C
else:
print 'Linear Combination Unexistent'
else:
print 'Linear Combination Unexistent'
Und das Ergebnis:
[[email protected] ejemplos python]# python lincomb.py
Scalar 1 = 3.0 Scalar 2 = -2.0
[7.0, 9.0, -8.0] = 3.0 * [1.0, 3.0, -2.0] + -2.0 * [-2.0, 0.0, 1.0]
[[email protected] ejemplos python]#
Zusammenfassend führt die grundlegende Vektoralgebra zu einer Reihe von Operationen, die lineare Gleichungssysteme und / oder einfache Arithmetik mit reellen Zahlen beinhalten. In einem weiteren Tutorial werden wir sehen, wie wir Produkte mit Vektoren entwickeln können, wie Skalarprodukt, Kreuzprodukt oder Mischprodukt.