Im vorherigen Tutorial haben wir die einfachen Schritte zum Lesen, Schreiben und Wiedergeben von Audiodateien gesehen. Wir haben sogar gesehen, wie wir eine Audiodatei aus einer periodischen Funktion wie der Kosinusfunktion synthetisieren können. In diesem Tutorial werden wir sehen, wie wir Signale hinzufügen, Signale multiplizieren (Modulation) und einige grundlegende mathematische Funktionen anwenden können, um ihre Auswirkungen auf das ursprüngliche Signal zu sehen.
Signale hinzufügen
Die Summe zweier Signale S1(t) und S2(t) ergibt ein Signal R(t), dessen Wert zu jedem Zeitpunkt die Summe der addierten Signalwerte zu diesem Zeitpunkt ist. Einfach so:
R(t) =S1(t) + S2(t)
Wir werden die Summe zweier Signale in Octave nachbilden und den Effekt grafisch sehen. Zuerst erzeugen wir zwei Signale mit unterschiedlichen Frequenzen, um das Signal zu sehen, das sich aus der Summe ergibt.
Schritt 1:Erstellen von zwei Signalen mit unterschiedlichen Frequenzen (ogg-Dateien)
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1,cos(w1),fs); %writing the function cos(w) on the files created
>> audiowrite(sig2,cos(w2),fs);
Hier werden wir beide Signale darstellen.
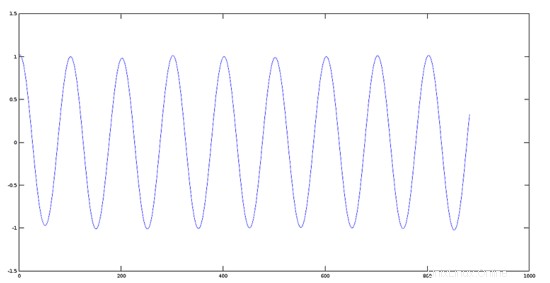
Plot von Signal 1 (440 Hz)
>> [y1, fs] = audioread(sig1);
>> plot(y1)
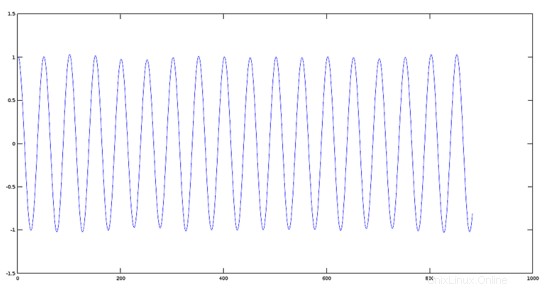
Plot von Signal 2 (880 Hz)
>> [y2, fs] = audioread(sig2);
>> plot(y2)
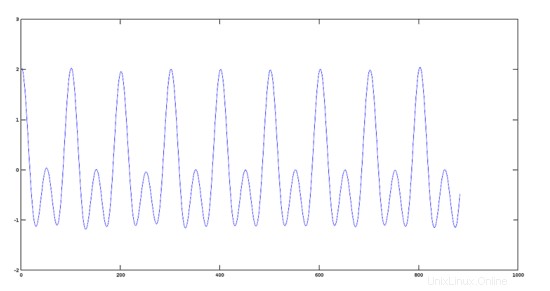
Schritt 2:Hinzufügen von zwei Signalen
Jetzt führen wir die Summe der beiden im vorherigen Schritt erstellten Signale durch.
>> sumres=y1+y2;
>> plot(sumres)
Darstellung des resultierenden Signals
Der Octaver-Effekt
Beim Octaver ist der von diesem Effekt erzeugte Klang charakteristisch, da er die vom Musiker gespielte Note emuliert, entweder in einer tieferen oder höheren Oktave (je nach Programmierung), gekoppelt mit dem Klang der Originalnote, dh es erscheinen zwei Noten identisch klingen.
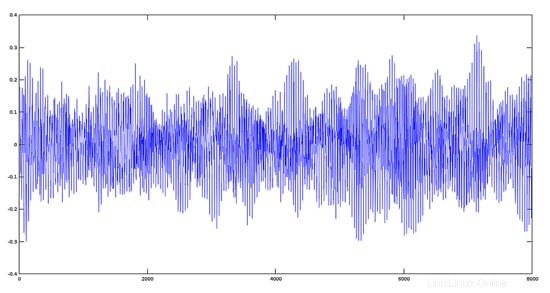
Schritt 3:Hinzufügen von zwei echten Signalen (Beispiel mit zwei Musiktiteln)
Zu diesem Zweck verwenden wir zwei Spuren von gregorianischen Gesängen (Voice Sampling).
Avemaria-Track
Zuerst wird ein Avemaria-Track gelesen und geplottet:
>> [y1,fs]=audioread('avemaria_.ogg');
>> plot(y1)
Hymnus-Track
Jetzt wird ein Hymnus-Track gelesen und gezeichnet
>> [y2,fs]=audioread('hymnus.ogg');
>> plot(y2)
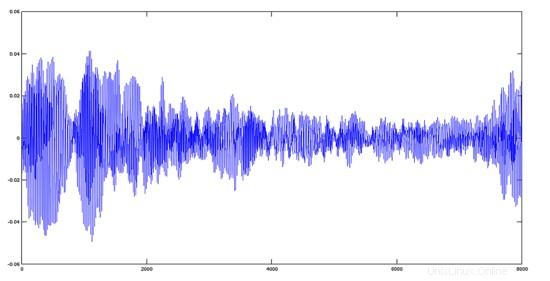
Avemaria + Hymnus-Track
>> y='avehymnus.ogg';
>> audiowrite(y, y1+y2, fs);
>> [y, fs]=audioread('avehymnus.ogg');
>> plot(y)
Das Ergebnis aus Audiosicht ist, dass beide Spuren klingt gemischt.
Produkt zweier Signale
Um zwei Signale zu multiplizieren, müssen wir analog zur Summe vorgehen. Lassen Sie uns dieselben zuvor erstellten Dateien verwenden.
>> sig1='cos440.ogg'; %creating the audio file @440 Hz
>> sig2='cos880.ogg'; %creating the audio file @880 Hz
>> product='prod.ogg'; %creating the audio file for product
>> fs=44100; %generating the parameters values (Period, sampling frequency and angular frequency)
>> t=0:1/fs:0.02;
>> w1=2*pi*440*t;
>> w2=2*pi*880*t;
>> audiowrite(sig1, cos(w1), fs); %writing the function cos(w) on the files created
>> audiowrite(sig2, cos(w2), fs);
>> [y1,fs]=audioread(sig1);
>> [y2,fs]=audioread(sig2);
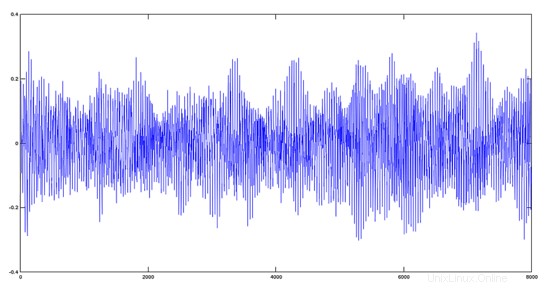
>> audiowrite(product, y1.*y2, fs); %performing the product
>> [yprod,fs]=audioread(product);
>> plot(yprod); %plotting the product
Hinweis:Wir müssen den Operanden '.*' verwenden, da dieses Produkt Wert für Wert aus den Argumentdateien erstellt wird. Weitere Informationen finden Sie im Handbuch für den Produktbetrieb mit Octave-Matrizen.
Plot des resultierenden Produktsignals
Grafischer Effekt der Multiplikation zweier Signale mit einem großen Grundfrequenzunterschied (Prinzipien der Modulation)
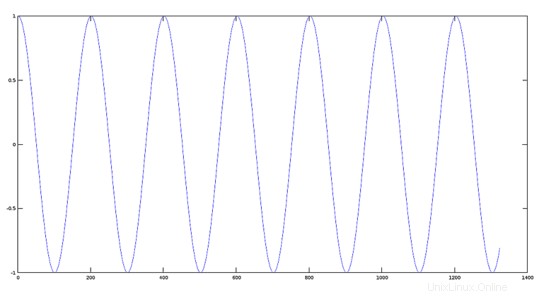
Schritt 1:
Erstellen Sie ein Tonfrequenzsignal mit einer Frequenz von 220 Hz.
>> fs=44100;
>> t=0:1/fs:0.03;
>> w=2*pi*220*t;
>> y1=cos(w);
>> plot(y1);
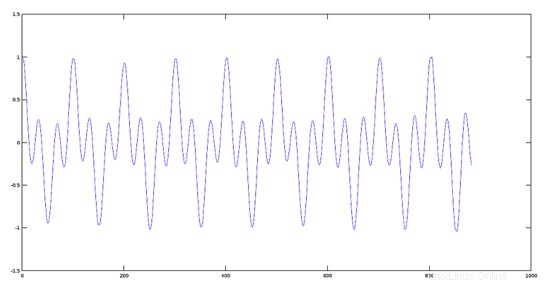
Schritt 2:
Erzeugen Sie ein höherfrequentes modulierendes Signal von 22000 Hz.
>> y2=cos(100*w);
>> plot(y2);
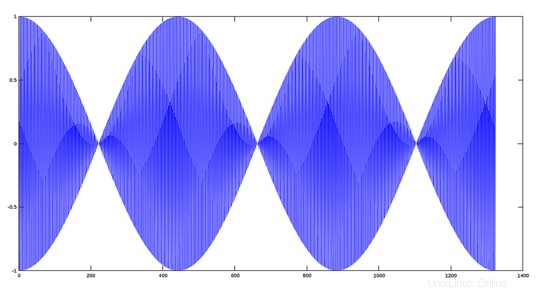
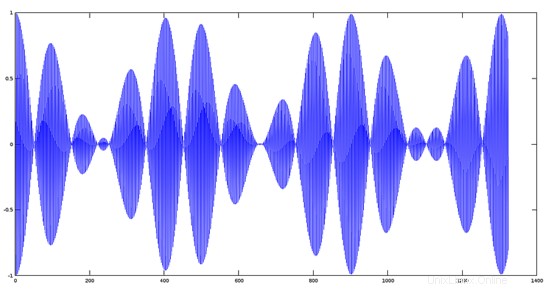
Schritt 3:
Multiplizieren und Plotten der beiden Signale.
>> plot(y1.*y2);
Multiplikation eines Signals mit einem Skalar
Der Effekt der Multiplikation einer Funktion mit einem Skalar entspricht der Änderung ihres Umfangs und in einigen Fällen des Vorzeichens der Phase. Bei einem Skalar K ist das Produkt einer Funktion F(t) durch den Skalar definiert als:
R(t) =K*F(t)>> [y,fs]=audioread('cos440.ogg'); %creating the work files
>> res1='coslow.ogg';
>> res2='coshigh.ogg';
>> res3='cosinverted.ogg';
>> K1=0.2; %values of the scalars
>> K2=0.5;
>> K3=-1;
>> audiowrite(res1, K1*y, fs); %product function-scalar
>> audiowrite(res2, K2*y, fs);
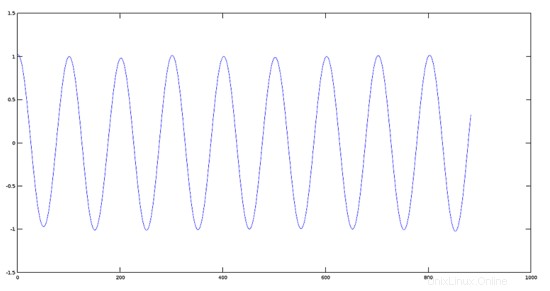
>> audiowrite(res3, K3*y, fs); Plot des Originalsignals
>> plot(y)
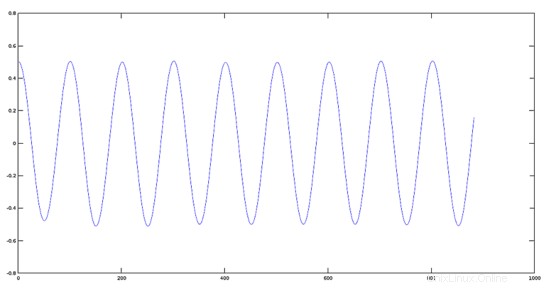
Plot eines um 0,2 reduzierten Signals
>> plot(res1)
Plot eines um 0,5 reduzierten Signals
>> plot(res2)

Plot eines Signals mit invertierter Phase
>> plot(res3)
Schlussfolgerung
Die grundlegenden mathematischen Operationen wie algebraische Summe, Produkt und Produkt einer Funktion durch einen Skalar sind das Rückgrat fortgeschrittenerer Operationen, darunter Spektrumanalyse, Amplitudenmodulation, Winkelmodulation usw. Im Folgenden Tutorial, werden wir sehen, wie man solche Operationen und ihre Auswirkungen auf Audiosignale durchführt.